Resoldre Sudoku

Mètodes de resoldre

L'estratègia per a resoldre un sudoku es pot considerar com la combinació de tres processos: escaneig, marcat i anàlisi.

Escaneig

L'escaneig es realitza des del principi i periòdicament, durant tota la resolució. L'escaneig consta de dues tècniques bàsiques: trama creuada i recompte, que poden usar-se alternativament.

Trama creuada:

Es tracta de l'escaneig de files (o columnes) per a identificar quina línia en una regió particular pot contenir un nombre determinat mitjançant un procés d'eliminació. Aquest procés es repeteix amb les columnes (o files).

Per a obtenir resultats més ràpids, els nombres són escanejats de forma ordenada, segons la seva freqüència d'aparició. És important realitzar aquest procés sistemàticament, comprovant tots els dígits del 1 al 9.

Recompte

Es tracta de buscar els dígits 1-9 per regions, files i columnes per a identificar nombres perduts.

El recompte basat en l'últim nombre descobert pot augmentar la velocitat de la recerca. També pot ser el cas (és típic en sudokus més difícils) que el valor d'una cel·la individual pugui ser determinat mitjançant un recompte invers, això és, escanejant la seva regió, fila o columna per a valors que no poden ser, per a veure quin és el que falta.

Els jugadors més avançats busquen contingències mentre escanegen, això és, fixen la ubicació d'un nombre en una fila, columna o regió o dues o tres cel·les. Quan aquestes cel·les estan totes en la mateixa fila (o columna) i regió, poden usar-se amb un propòsit d'eliminació durant la trama creuada i el recompte. Els sudokus particularment desafiadors poden requerir el reconeixement de múltiples contingències, potser en múltiples adreces o fins i tot interseccions relegant la majoria dels resolutors al marcat (com es descriu més a baix).

Els sudokus que poden ser resolts només mitjançant escaneig, sense requerir la detecció de contingències es classifiquen com sudokus fàcils; altres sudokus més difícils, per definició, no poden resoldre únicament mitjançant escaneig.

Marcat

L'escaneig s'atura quan no podem descobrir nous nombres. En aquest punt és necessari centrar-se en alguna anàlisi lògica. La majoria troba útil guiar aquesta anàlisi mitjançant el marcat de nombres candidats en les cel·les buides. Hi ha dues notacions populars: subíndexs i punts.

Subíndex:

Els nombres candidats s'escriuen en petit en les cel·les. El desavantatge és que els puzles originals són publicats en periòdics que habitualment no deixen massa espai per a acomodar més d"uns pocs dígits. Si s'utilitza aquesta notació, els resolutors creen, sovint, una còpia més gran del puzle i empren un llapis afilat.

Punts:

Es basa en un patró de punts amb un punt en el cantó superior esquerra representant un 1 i un punt en el cantó inferior dreta representant un 9. Aquesta notació té com a avantatge que pot usar-se en el puzle original. Es requereix destresa per a l'emplaçament dels punts, perquè punts desplaçats o marques distretes duen, inevitablement, a confusió i no són fàcils d'esborrar sense afegir més confusió.

Anàlisis:

Hi ha dues tècniques d'anàlisis principals: Eliminació i "i si...?".

Eliminació:

L'anàlisis es realitza mitjançant la successiva eliminació de nombres candidats per a una o més cel·les, fins a deixar només una elecció.

Després d'assolir cada resposta, ha de realitzar-se un nou escaneig (habitualment comprovant l'efecte de l'últim nombre). Hi ha una sèrie de tàctiques d'eliminació. Una de les més comunes és el "esborrat del candidat no coincident". Les cel·les amb idèntica configuració de nombres candidats es diu que coincideixen si la quantitat de nombres candidats en cadascuna és igual al nombre de cel·les que els contenen.

Per exemple, es diu que cel·les coincideixen amb una particular fila, columna o regió si dues cel·les contenen el mateix parell de nombres candidats (p, q) i no altres, o si tres cel·les contenen el mateix triplet de nombres candidats (p, q, r) i no altres. Aquestes són, essencialment, contingències coincidents. Aquests nombres (p, q, r) que apareixen com candidats en qualsevol lloc en la mateixa fila, columna o regió en cel·les no coincidents, poden ser esborrats.

I si...?:

Es basa a seleccionar una cel·la amb només dos nombres candidats i es realitza una conjectura. Les etapes de dalt es repeteixen tret que es trobi una duplicació, en aquest cas el candidat alternatiu és la solució. En termes lògics aquest mètode es coneix com reducció a l'absurd.

Nishio és una forma limitada d'aquesta tècnica d'anàlisis: Per a cada candidat d'una cel·la, es pregunta: ¿Aquest nombre pot anar a una altra cel·la? Si la resposta és sí, llavors aquest candidat pot ser eliminat.

Idealment, es necessita trobar una combinació de tècniques que evitin algun dels inconvenients dels elements de dalt. El recompte de regions, files i columnes pot resultar avorrit. Escriure nombres candidats en cel·les buides pot consumir massa temps. La tècnica "i si...?" pot ser confusa tret que siguis molt organitzat. El quid de la qüestió és trobar una tècnica que minimitzi el recompte, el marcat i l'esborrat.

Nivell principiant

• Exemple 1

  • ¿On es pot posar l'1 al quadrat (3×3) esquerre?

    

  • L'1 ja està en la fila superior i mitjana.

    

  • Així doncs, solament pots posar-lo a

    

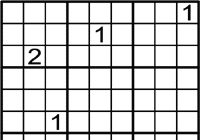
• Exemple 2

  • Com fer-lo?

    

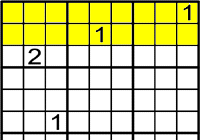
  • No pot jutjar on col·locar-lo solament amb les files.

    

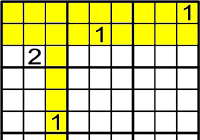
  • Mira la columna, llavors...

    

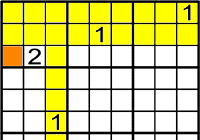
  • Ara ja pots col·locar-lo a

    

• Exemple 3

  • On pots posar l'1 al quadrat d'alt-esquerre?

    

  • Mira les files al principi.

    

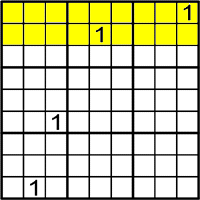
  • Llavors, mira les columnes.

    

  • En aquest cas solament pots posar-lo a .

    

• Exemple 4

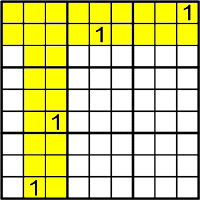
  • On pots posar l'1 al quadrat d'alt-esquerre.
    Aquest patró és fácil i important.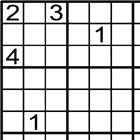

    

  • Primer de tot mira la fila en aquest cas.

    

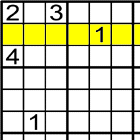
  • Després mira les columnes.

    

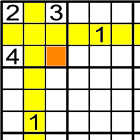
  • En aquest cas solament hi ha una solució .

    

• Exemple 5

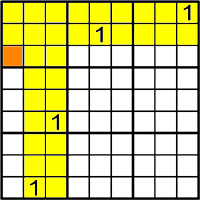
  • Aquest és un altre patró.
    On es posarà l'1 en el quadrat d'alt-esquerre.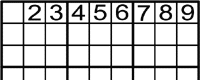

    

  • En aquesta fila hi ha els números del 2 al 9.

    

  • Per tant, l'1 solament pot anar en .

    

Nivell intermedi

• Exemple 1

  • On pots posar l'1?

    

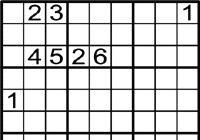
  • Primer mira les files i les columnes on hi ha un 1.

    

  • L'1 pot anar a dos llocs , per ara no podem posar-lo.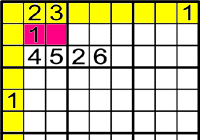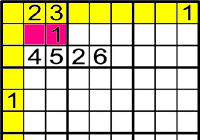

    

  • Però si sabem que han d'anar en aquesta fila.

    

  • Per això l'1 solament pot anar aquí .

    

• Exemple 2

  • On podem posar l'1?

    

  • Abans mira si hi ha algun 1 que t'afecti.

    

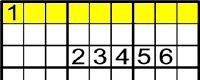
  • Ara sabem que l'1 ha d'anar en la fila del mig .

    

  • Gràcies a això, podem descartar una fila més.

    

  • Així doncs, solament pot anar en un lloc .

    

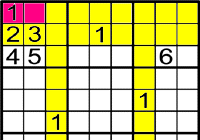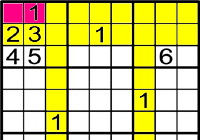
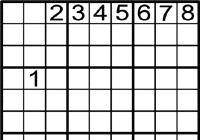
• Exemple 3

  • A poc a poc, es va complicant però no et preocupes. Recorda l'exemple 2 del principiant.
    On pots posar l'1?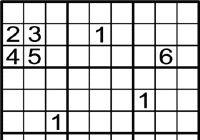

    

  • Mira les files i columnes, en aquest cas l'1 solament pot anar en la fila de dalt .

    

  • Per tant, l'1 solament pot anar en un lloc .

    

• Exemple 4

  • On pot anar l'1?

    

  • Pot anar en els dos .
    Has de mirar les columnes.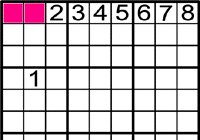

    

  • 1 solament pot anar a

    

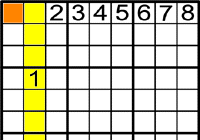
  • Quin número anirà a l'altra ?

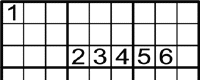
• Exemple 5

  • On poden anar l'1, el 8 i el 9?

    

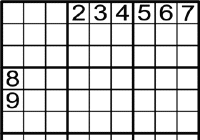
  • En la fila superior hi ha els números del 2 al 7.
    Això vol dir que l'1, el 8 i el 9 van en les tres

    

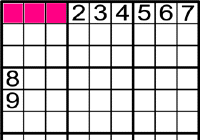
  • En la columna esquerra hi ha els números 8 i 9.
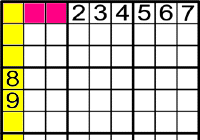
    Per això, el 8 i el 9 han d'anar a les .

    

  • Després d'això l'1 solament pot anar a

    

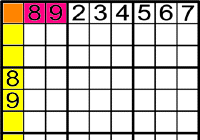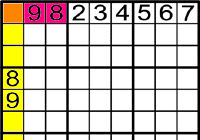
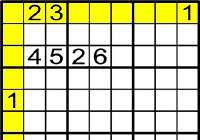
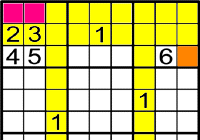
Nivell expert

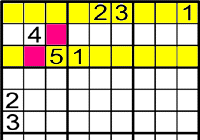
• Exemple 1

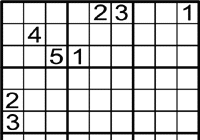
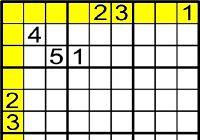
  • On poden anar el 2 i 3?

    

  • Has de mirar les files i columnes.

    

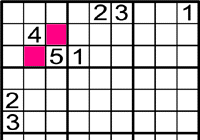
  • El 2 i el 3 han d'anar als

    

  • Ara mira on pot anar l'1.

    

  • L'1 solament pot anar a . Perquè els altres estan ocupats.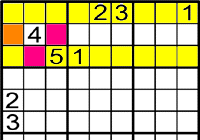

    

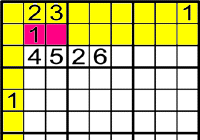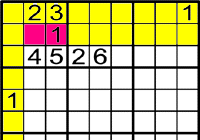
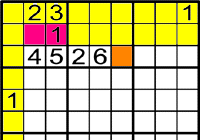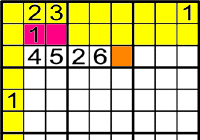
• Exemple 2

  • On pot anar l'1?

    

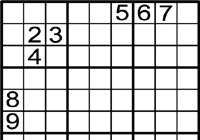
  • El 1 és l'únic número que pot anar a , ja que els números del 5 al 9 no poden anar per la raó que estan en la mateixa fila o columna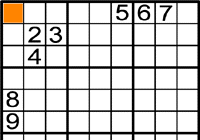